ECDSA
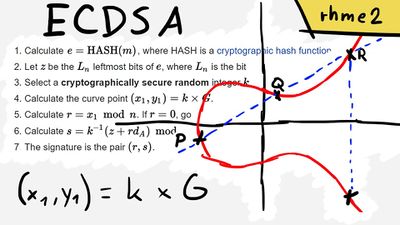
ECDSA (Elliptic Curve Digital Signature Algorithm — Алгоритм цифровой подписи на эллиптической кривой) — это криптографический алгоритм, используемый Биткоином для гарантии того, что средства могут быть потрачены только их законными владельцами.
Содержание
О ECDSA
Сравнение размера ключа и подписи с DSA
Как и в случае криптографии с эллиптическими кривыми, размер бит открытого ключа, который, как полагают, необходим для ECDSA, примерно в два раза превышает уровень безопасности в битах. Например, при уровне безопасности 80 битов (то есть злоумышленнику требуется максимум около 280 операций для поиска закрытого ключа) размер открытого ключа ECDSA будет равен 160 битам, тогда как размер открытого ключа DSA по меньшей мере равен 1024 бита С другой стороны, размер подписи одинаков как для DSA, так и для ECDSA: примерно 4t бит, где t — уровень безопасности, измеренный в битах, то есть около 320 бит, для уровня безопасности 80 бит.
Концепты
Несколько понятий, связанных с алгоритмом цифровой подписи на эллиптической кривой:
- Закрытый ключ: секретный номер, известный только тому, кто его сгенерировал. Закрытый ключ — это, по сути, случайное число. В Биткоине тот, у кого есть закрытый ключ, соответствующий средствам в публичной книге, может их потратить. В биткоинах закрытый ключ представляет собой одно беззнаковое 256-битное целое число (32 байта).
- Открытый ключ: число, которое соответствует закрытому ключу, но не должно храниться в секрете. Открытый ключ может быть рассчитан из личного ключа, но не наоборот. Открытый ключ может использоваться для определения подлинности подписи (другими словами, созданной с использованием надлежащего ключа), не требуя разглашения личного ключа. В Биткоине открытый ключ является сжатым или несжатым. Сжатые открытые ключи имеют размер 33 байта и состоят из префикса 0x02 или 0x03 и 256-разрядного целого числа, называемого x. Старые несжатые ключи имеют размер 65 байт, состоящий из постоянного префикса (0x04), за которым следуют два 256-битных целых числа, называемых x и y (2*32 байта). Префикс сжатого ключа позволяет получить значение y из значения x.
- Подпись: число, которое доказывает, что была подписана операция. Подпись математически генерируется из хэша чего-либо, что должно быть подписано, плюс закрытый ключ. Сама подпись состоит из двух чисел, известных как r и s. С открытым ключом можно использовать математический алгоритм для подписи, чтобы определить, что он изначально был получен из хеша и закрытого ключа, без необходимости знать закрытый ключ. Подписи имеют длину 73, 72 или 71 байт с вероятностями приблизительно 25%, 50% и 25% соответственно, хотя размеры даже меньше, чем это возможно с экспоненциально уменьшающейся вероятностью.
Безопасность
В декабре 2010 года группа, называющая себя fail0verflow, объявила о восстановлении закрытого ключа ECDSA, используемого Sony для подписи программного обеспечения для игровой консоли PlayStation 3. Однако эта атака сработала только потому, что Sony неправильно реализовала алгоритм, потому что k было константой, а не случайным числом. Как указывалось в разделе алгоритма генерации подписи выше, это делает dA разрешимым, а весь алгоритм бесполезным.
29 марта 2011 года два исследователя опубликовали документ IACR, демонстрирующий, что можно извлечь закрытый ключ TLS сервера, используя OpenSSL, который аутентифицируется с помощью Elliptic Curves DSA через двоичное поле с помощью временной атаки. Уязвимость была исправлена в OpenSSL 1.0.0e.
В августе 2013 года было обнаружено, что ошибки в некоторых реализациях Java-класса SecureRandom иногда приводили к коллизиям в значении k. Это позволило хакерам восстановить закрытые ключи, предоставив им тот же контроль над транзакциями биткоинов, что и владельцы законных ключей, используя тот же эксплойт, который использовался для выявления ключа подписи PS3 в некоторых реализациях приложений Android, которые используют Java и полагаются на ECDSA для аутентификации транзакций.
Эту проблему можно предотвратить с помощью детерминированной генерации k, как описано в RFC 6979.